Geometry, the branch of mathematics that deals with shapes, sizes, and properties of figures, relies on fundamental principles to establish relationships between various geometric elements. One such principle is the Angle Addition Postulate, which provides a simple and powerful tool for calculating the sum of angles.
The Angle Addition Postulate states that the larger of two adjacent angles can be calculated by adding their respective measures. By subtracting the larger angle from the smaller angle given, we can use the postulate to determine the size of one of the smaller angles.
The Angle Addition Postulate states that if you have two adjacent angles, then the measure of the larger angle is equal to the sum of the measures of the smaller angles. In other words, when two angles share a common vertex and a common side, the total measure of the larger angle is the sum of the measures of the two smaller angles.
To better understand the Angle Addition Postulate, let’s consider a simple example. Suppose we have two adjacent angles, angle AOC and angle COB, sharing a common vertex O and a common side OC. We want to find the measure of the larger angle AOB.
Angle Addition Postulate Formula
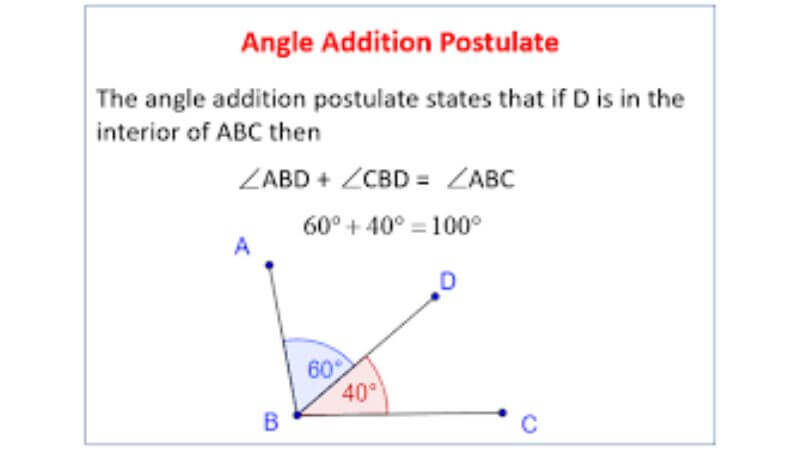
The Angle Addition Postulate formula states that if D is in the interior of ∠ABC then ∠ABD +∠DBC = ∠ABC.Measures of adjacent angles can be used in the formula. When two smaller angles add up to form a larger one, the larger angle is the result.
The formula for the Angle Addition Postulate has two applications:
- The larger of two adjacent angles must be calculated.
- Given the larger measure and the measure of the other adjacent angle, find the missing measure of one of the adjacent angles.
Without actually measuring the angle, the previous figure allowed us to calculate its value by adding the two smaller given angles.
The formula can also be used to determine the missing angle measurement by utilizing information about an adjacent angle. Subtracting the measure of the smaller adjacent angle from the larger angle yielded the missing measure in the following illustration.
Using the Angle Addition Postulate, we know that the measure of angle AOB is equal to the sum of the measures of angle AOC and angle COB. Mathematically, we can express this as:
m∠AOB = m∠AOC + m∠COB
Here, “m∠” denotes the measure of an angle. By substituting the known values of the measures of angles AOC and COB into the equation, we can determine the measure of angle AOB.
The Angle Addition Postulate is not only useful for finding the sum of adjacent angles, but it also has broader applications in geometry. For instance, it can be applied to solve problems involving polygons, where the angles are not necessarily adjacent but are part of the same figure.
Consider a polygon with n sides. To find the sum of all the interior angles of the polygon, we can divide it into (n-2) triangles by drawing diagonals from a single vertex. Each triangle has an interior angle sum of 180 degrees. Since the angles at the vertex are shared by two adjacent triangles, the total sum of the interior angles of the polygon can be calculated using the Angle Addition Postulate:
Sum of interior angles = (n-2) × 180 degrees
This formula is a direct result of applying the Angle Addition Postulate to each vertex of the polygon.
In addition to its practical applications, the Angle Addition Postulate also helps establish the foundation for more advanced concepts in geometry, such as angle bisectors and angle congruence. By understanding the relationship between angles and their measures, we can explore further geometric principles and theorems.
Frequently Asked Questions
How do you do angle addition postulate?
To apply the Angle Addition Postulate, determine the sum of the two adjacent angles to find the measure of the larger angle they form together.
What is the angle addition postulate in math?
The Angle Addition Postulate in math states that the sum of two adjacent angle measures will equal the measure of the larger angle that they form.
Final Thoughts on Angle Addition Postulate
In conclusion, the Angle Addition Postulate is an important tool in geometry that enables us to calculate the sum of angles when those angles share a common vertex and side.
This makes the Angle Addition Postulate an extremely useful tool. This postulate serves as the foundation for a wide variety of geometric calculations and proofs.
For example, it can be used to determine the sum of the interior angles in polygons, as well as the measure of the angles that are adjacent to each other. We will be able to delve deeper into the fascinating world of geometry and its intricate relationships between shapes and angles once we have mastered this fundamental principle.
Also Read: 10 Ways To Understand the Identity Property of Addition in Math
Tinydale is on YouTube, Click here to subscribe for the latest videos and updates.
Follow Us: Facebook | Instagram | Twitter | Youtube | Pinterest

